Essentiellement, la loi de Pascal stipule qu'un changement de pression en tout point d'un fluide incompressible et en vase clos est transmis intégralement et sans diminution à toutes les portions de ce fluide. Cela signifie que si vous poussez un fluide dans un récipient scellé, la pression augmente partout à l'intérieur de ce récipient de la même quantité exacte, au même moment exact.
Bien que la définition se concentre sur la transmission de la pression, la véritable puissance de la loi de Pascal réside dans la façon dont elle nous permet d'obtenir une multiplication de force massive. Ce principe unique est le fondement de presque tous les systèmes hydrauliques modernes.
L'équation fondamentale : Pression, Force et Surface
Pour saisir les implications de la loi de Pascal, vous devez d'abord comprendre la relation entre ses trois composants fondamentaux.
Définition de la Pression
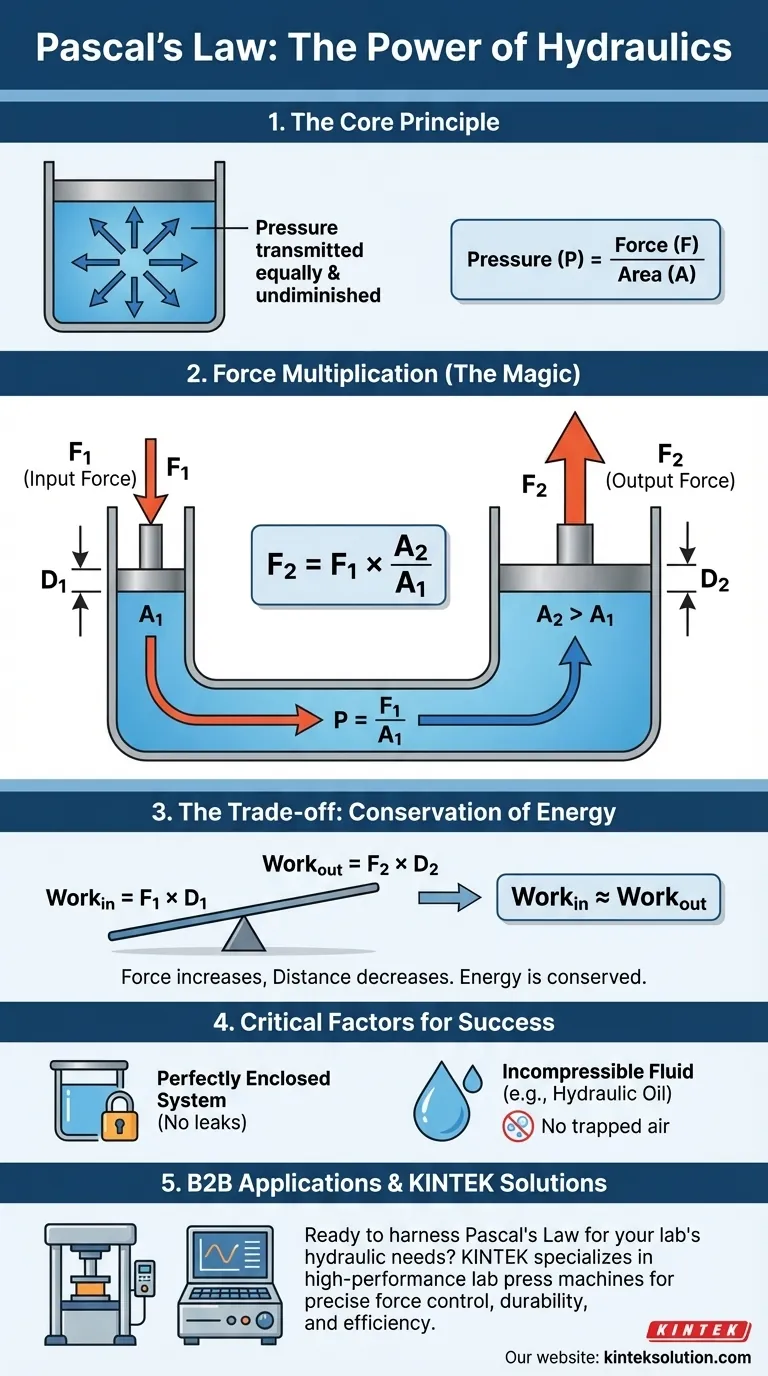
La pression (P) est définie comme une Force (F) appliquée sur une Surface (A) spécifique. L'équation est P = F/A.
Pensez à la différence entre quelqu'un qui vous pousse avec la paume ouverte et quelqu'un qui vous pousse avec un seul doigt. La force peut être la même, mais la pression du bout du doigt est bien plus grande car elle est concentrée sur une surface beaucoup plus petite.
Le rôle d'un fluide incompressible
La loi de Pascal repose sur l'utilisation d'un fluide incompressible, comme l'eau ou l'huile hydraulique. Lorsque vous appliquez une force à ce type de fluide, il ne se comprime pas en un volume plus petit.
Parce que le fluide ne peut pas être comprimé, l'énergie que vous introduisez doit être transmise ailleurs. C'est ainsi que la pression se propage instantanément dans tout le système.
La magie de la multiplication de force
Le véritable génie de l'application de la loi de Pascal n'est pas seulement que la pression est transmise, mais qu'elle peut être exploitée pour multiplier la force. C'est le principe de fonctionnement de tout, du cric de voiture au train d'atterrissage d'un avion.
Le modèle hydraulique de base
Imaginez un tube en U rempli d'huile, scellé aux deux extrémités par des pistons. Un piston est petit (le piston d'entrée), et l'autre est grand (le piston de sortie).
Application de la force d'entrée
Disons que vous appliquez une petite force descendante (F1) sur le petit piston, qui a une surface A1. Cela crée une pression dans le fluide : P = F1 / A1.
Transmission de la pression
Selon la loi de Pascal, cette pression exacte (P) est maintenant présente partout dans le fluide. Cela inclut la zone directement sous le grand piston de sortie.
Calcul de la force de sortie
Cette même pression (P) pousse maintenant vers le haut sur le grand piston, qui a une surface A2. La force ascendante résultante (F2) est F2 = P x A2.
Puisque la pression est la même partout (F1/A1 = F2/A2), vous pouvez constater que la force de sortie est proportionnelle au rapport des surfaces. Si la surface du piston de sortie est 10 fois plus grande que la surface du piston d'entrée, la force de sortie sera 10 fois supérieure à la force que vous avez appliquée.
Comprendre les compromis
Cette multiplication de force ne vient pas de nulle part ; elle suit les lois de la physique et implique des compromis critiques.
Conservation de l'énergie
Vous ne pouvez pas créer de l'énergie à partir de rien. Bien que la force de sortie soit multipliée, la distance parcourue par le piston de sortie est proportionnellement réduite.
Pour soulever le grand piston de 1 pouce, vous devrez peut-être pousser le petit piston de 10 pouces. Le travail effectué (Force x Distance) reste le même des deux côtés, en ignorant le frottement.
L'importance d'un système "fermé"
Le principe de Pascal ne fonctionne que dans un système parfaitement étanche. Toute fuite entraînera l'échappement du fluide lorsque la pression est appliquée, dissipant la pression et entraînant une défaillance du système.
Les propriétés du fluide sont importantes
Bien que nous supposions souvent un fluide idéal et incompressible, les fluides hydrauliques réels ont une viscosité (résistance à l'écoulement) et peuvent contenir des bulles d'air piégées. L'air est hautement compressible, et sa présence dans les conduites hydrauliques peut rendre le système "spongieux" et réduire considérablement son efficacité.
Comment appliquer cela à votre projet
Comprendre le principe vous permet de concevoir et de dépanner efficacement les systèmes. Votre objectif spécifique déterminera quel aspect de la loi est le plus important.
- Si votre objectif principal est l'avantage mécanique : Concentrez-vous sur la maximisation du rapport de surface entre les pistons de sortie et d'entrée (A2/A1) pour obtenir la multiplication de force souhaitée pour une presse ou un cric de levage.
- Si votre objectif principal est l'efficacité du système : Donnez la priorité à la création d'un système parfaitement étanche et à l'utilisation d'un fluide incompressible de haute qualité pour minimiser les pertes d'énergie dues aux fuites ou à la compression interne.
- Si votre objectif principal est un contrôle précis : Tirez parti du compromis de travail ; un petit mouvement gérable à l'entrée peut se traduire par un très petit mais puissant et précis mouvement à la sortie, ce qui est idéal pour des systèmes comme les freins de véhicule.
En comprenant ce principe, vous passez de la simple connaissance d'une définition à la compréhension de la puissance élégante derrière toute l'ingénierie hydraulique.
Tableau récapitulatif :
| Aspect | Idée clé |
|---|---|
| Définition | Le changement de pression dans un fluide incompressible est transmis également et sans diminution. |
| Multiplication de force | La force de sortie augmente avec le rapport de surface (F2 = F1 × (A2/A1)). |
| Compromis | Le gain de force réduit la distance parcourue ; l'énergie est conservée. |
| Applications | Utilisé dans les vérins hydrauliques, les presses et les systèmes de contrôle de précision. |
Prêt à exploiter la loi de Pascal pour les besoins hydrauliques de votre laboratoire ? KINTEK est spécialisé dans les machines de presse de laboratoire haute performance, y compris les presses de laboratoire automatiques, les presses isostatiques et les presses de laboratoire chauffées. Notre équipement assure un contrôle précis de la force, une durabilité et une efficacité pour vos applications de laboratoire. Contactez-nous dès aujourd'hui pour discuter de la manière dont nos solutions peuvent optimiser vos projets et augmenter votre productivité !
Guide Visuel
Produits associés
- Presse hydraulique automatique à haute température avec plaques chauffantes pour laboratoire
- Presse de laboratoire hydraulique manuelle chauffée avec plaques chauffantes intégrées Presse hydraulique
- Presse hydraulique chauffante avec plateaux chauffants pour boîte à vide de laboratoire
- Presse hydraulique de laboratoire 2T Presse à granuler de laboratoire pour KBR FTIR
- Presse hydraulique de laboratoire pour boîte à gants
Les gens demandent aussi
- Pourquoi une presse hydraulique de laboratoire avec plaques chauffantes est-elle nécessaire pour les films PLA/TEC ? Obtenir une intégrité précise de l'échantillon
- Quelles sont les applications industrielles des presses hydrauliques chauffantes ? Maîtriser la chaleur et la force pour une fabrication de précision
- Comment la température de la plaque chauffante est-elle contrôlée dans une presse de laboratoire hydraulique ? Atteindre une précision thermique (20°C-200°C)
- Pourquoi une presse hydraulique chauffante de laboratoire est-elle nécessaire pour les éprouvettes en PVC ? Assurer des données précises de traction et de rhéologie
- Quel rôle joue une presse hydraulique chauffante dans les tests et la recherche sur les matériaux ? Perspectives essentielles pour l'innovation en laboratoire
